• ポリテクカレッジ北海道（北海道職業能力開発短期大学校）寺島　周平

機械設計では，設計者は自らの判断でその値を決めることのできるパラメータを増減させた設計試案をいくつか用意して，その中で望ましいものを選択する方法を繰り返す。どのような初期値を与えれば望ましい設計が得られるかは，経験と直感が頼りである。与えられた制約条件がより複雑になる場合，膨大な時間を費やす作業であり，危険で誤った方向に至ることが多い。最も合理的な設計を求めるためには，計算機に設計案を用意させる必要がある。例えば，強度計算の結果として計算された応力や変位を最初に与えて，それらを満足するような寸法を自動的に決定する。

企業で広く導入されている汎用CAEには構造最適化のオプションが備えられているが，CADを用いて対象となる構造のモデリングを実施した後，設計変数の関連づけや拘束条件の指定を行わねばならない。そのため，有限要素解析を利用しない簡単な最適設計に対しては，モデリングや操作の習得が煩雑になる。汎用CAEはブラックボックスとしての使用を考えて開発されているため，メーカー独自の最適化システムへの組み込みやカスタマイズは容易ではない。

他には，オペレーションズリサーチ(OR)のソフトを設計問題に利用することも考えられるが，有限要素法を連結するために適したインタフェースやアルゴリズムを備えているものが少なく，現実的な計算時間内に最適解を得ることは難しい。

以上のような状況から，CAEの最適化機能とは別途に汎用の最適化ツールを備えておくことが必要になると考えられる。さらに，企業が独自の最適化システムを構築するためにも撮適化ツールは必須のものである。このようなソフトウェアとしては著者が開発を進めている汎用オプティマイザ1)が最適であろう。

ここでは開発した設計最適化を目的とした汎用オプティマイザを紹介して，コイルばねの設計問題を通じてプログラムの有用性を示す。プログラムは，企業ユーザの要求を満たす汎用性があり，パソコン(PC)からワークステーションまでの広い範囲の機種に対応することができる。高い信頼性をもつ使いやすいツールを企業に対して提供することにより，設計の意思決定を支援することができる。

２．１　一般的な最適化問題の定式化

設計最適化は，最初に設計問題を定式化した後，システムを最適化するためのアルゴリズムを適用して反復計算を繰り返し，最適解に収束するまで設計点の数列を発生する。最初に最適化問題の一般的な定式化を行う。

設計変数ベクトルXの上下限をXU，XL，目的関数をf(X)，ｊ番目の非線形制約条件をgj(X)とすると，一般化された非線形計画問題を次のように表すことができる。ここでは上下限制約条件式を非線形制約条件と区別する。非線形制約条件の総数をｍ個，設計変数の総数をｎ個とする。

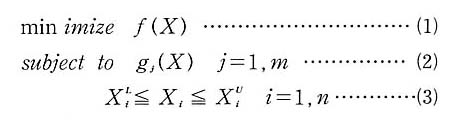
目的関数f(X)はXの非線形関数とする。目的関数と非線形制約条件式を現在の設計点X0の回りで，1次の導関数の項までテイラー展開し，近似最適化問題を(4)～(6)式のように構成する。プログラムでは原問題を線形化して，現在の設計点に関する新しい線形化問題を構成するプロセスを繰り返して正確な解を得ることができる。

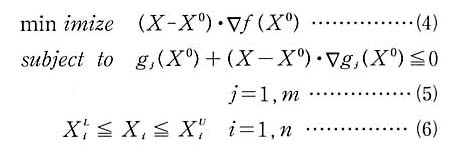
テイラー級数展開を評価する設計点を明確にするために上つき添字の0を付加する。設計点における関数値とその勾配が一定であるから，(4)～(6)式は，設計変数ベクトルXの変化分に対する線形計画問題を構成することができる。

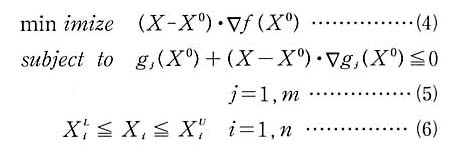
小さい定数εに対して(7)式が成り立つとき，最適解が得られたものとして計算を終了する。

２．２　プログラムの説明

プログラムの開発における基本方針は以下のとおりである。

1. ①　構造撮適化の問題を解くことを目的とした汎用オプティマイザの開発。
2. ②　プログラムの有効利用を支援するドキュメントの整備。
3. ③　Fortranソースコードを提供して，ユーザによるカスタマイズを容易にする。
4. ④　PCからワークステーションまでの幅広い領域の機種をカバーして，あらゆるシステム環境下において常に一定の能力を発揮できるようにする。

一般の最適化問題では最適解に近づくに従って，設計変数のいくつかがゼロまたは無限大に近づくことがある。このような場合，実際のプログラムではオーバフローまたはアンダフローを引き起こす。そのため，無限小または無限大をマシンに依存した非常に小さい数，または非常に大きい数として設定しなければならない。

オプティマイザは実用的で信頼性のある暴適化アルゴリズムを複数採用することが必要である。解の改良過程を途中で打ち切らなければならない場合，あるいは最終的な最適解が受け入れられないとき，最適点により近いものや許容解に近い中間解を選択することができるようにライブラリには逐次線形計画法2)および，内接超球法3)のアルゴリズムを備えておく。

以上のような基本方針をもとにしてプログラムの設計・開発を行った。図１にオプティマイザの概念を示す。

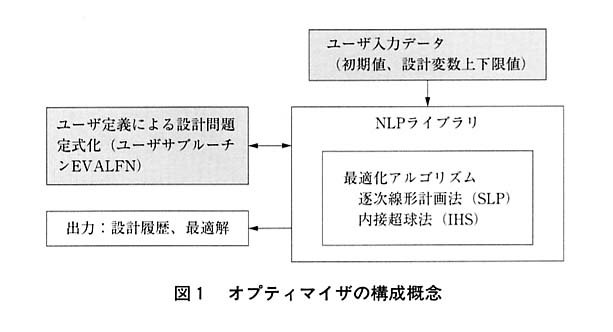
プログラムはFortran77の基本的な命令を用いて記述されている。そのため，安価なMS-DOSマシンからUNIXワークステーションまでのさまざまなシステム環境で，同一のソースコードをコンパイルすることが可能である。プログラムはメインプログラムと利用者からみてブラックボックスとして扱える複数のサブルーチンから構成されている。図２にメインプログラムのフローチャートを示す。

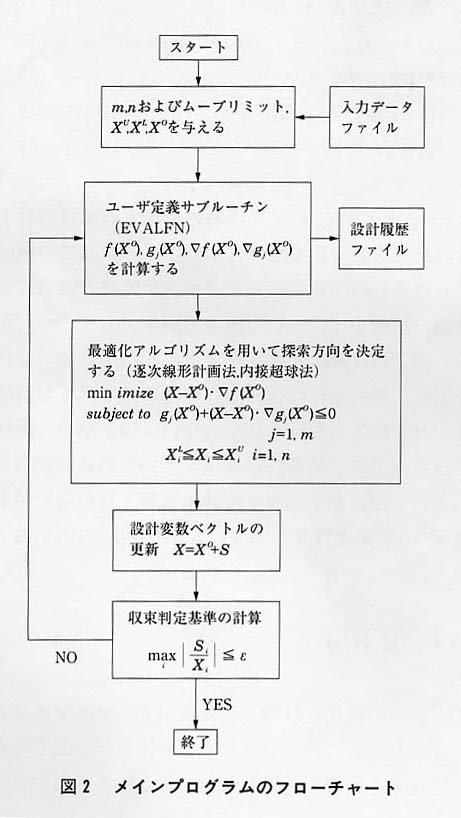
メインプログラムではいわゆるダイナミックアロケーションにより配列を割り当てる。メインプログラムの先頭に書かれた以下の2行を変更して，利用者が配列を新たに宣言・拡張することができる。変数MTOTはワードで表示したワークエリアの総数である。COMMON文で宣言される配列の最大値はMTOT+1にする。

COMMON A(10001)

MTOT=10000

プログラムの実行に先立って，利用者は設計問題の定式化を記述したサブルーチンを準備しなければならない。このサブルーチンでは，目的関数と制約関数および設計変数に関するそれらの導関数をFortranによりコーディングする。サブルーチン名はEVALFNである。(8)～(12)式により表される例題に対するユーザ作成サブルーチンを図３に示す。

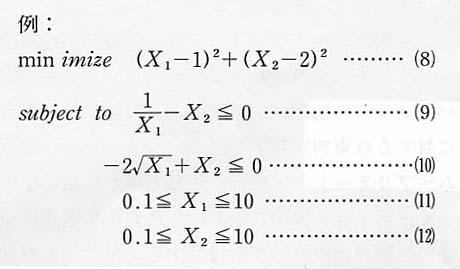
ユーザサブルーチンは引数の受け渡しの規約に従って，利用者が容易に変更・拡張することができる。作成したユーザサブルーチンとオプティマイザを構成する他のモジュールをmakeなどのツールを用いてコンパイル・リンクを行い，実行形式ファイルを生成する。ユーザサブルーチン以外のモジュールについても，利用者がアルゴリズムに介入したり，変更することが可能である。

次に，入力データをフリーフォーマット形式で準備する。(8)～(12)式の例題に対するユーザ作成データファイルの内容を図４に示す。

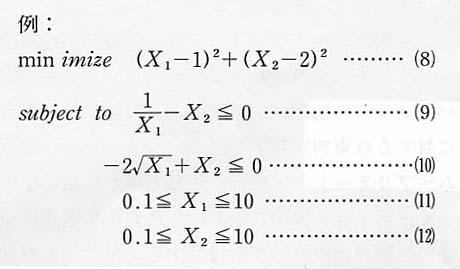
この入力データファイルでは，非線形制約関数と設計パラメータの総数およびムーブリミット，設計パラメータの初期値，下限値と上限値，プログラムに対する収束判定基準などのパラメータを与える。ムーブリミットとは振動が生じて解が収束しない場合や，テイラー展開による線形近似の精度が悪い場合に，線形近似の精度を保証する手段として移動制約を設定するためのパラメータである。

本項ではオプティマイザをコイルばねの重量最小化設計4)に適用した例を示す。コイルばねの設計では，設計者は外荷重を仮定して，ばねの線径，平均半径や有効巻数を変化させて，許容応力やサージングの周波数の制限を満足するかどうかを判断する。例題に対するユーザサブルーチンと入力データを作成した後，汎用オプティマイザに備わる内接超球法を用いて最適化を実施した。文献4)の結果と比較するために，US慣用単位系を用いた。諸記号は文献4)に準ずるものを使用し，定式化の詳細は省略する。

外荷重：Ｐ＝10 lbs

せん断弾性係数：Ｇ＝1.15×10 7lb/in2

ばねの最小伸び：△0.5in

ばねの重量密度：ρ＝7.38342×10-4lb-sec2/in4

許容せん断応力：τa＝8.0×10 4lb/in2

サージングの振動数:ω

サージングの振動数に対する下限値：ω0=100Hz

ばねののび: δ

設計変数はばねの線径d(in)

平均半径D(in)

有効巻数N　　　　　　　　とする。

設計には最小伸び，せん断応力およびサージング周波数に対する制約条件を考慮する。非線形の制約条件を(13)～(15)式に示す。また，線形の制約条件を(16)式に示す。設計変数に対する上下限制約式は(17)～(19)式のとおりである。

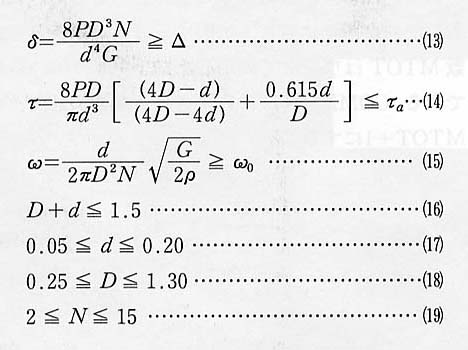
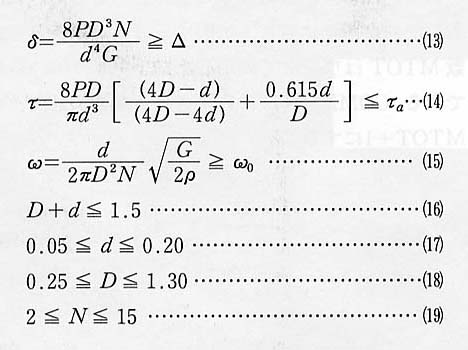
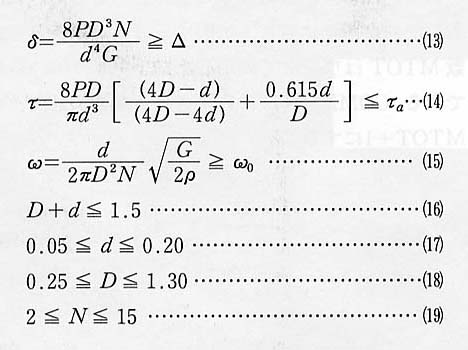
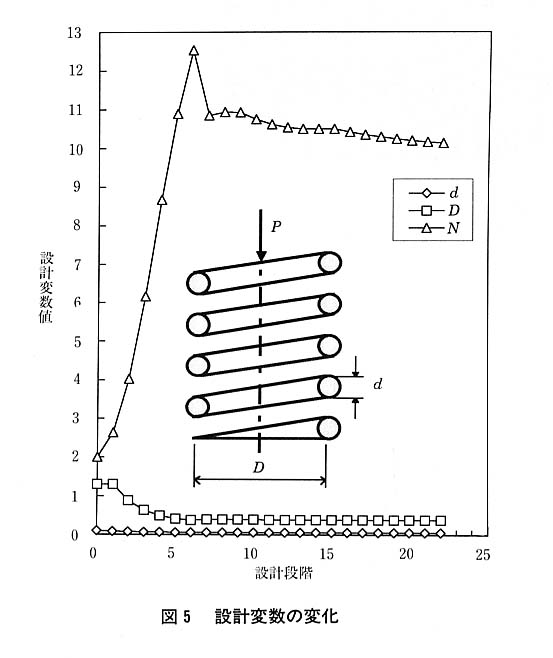
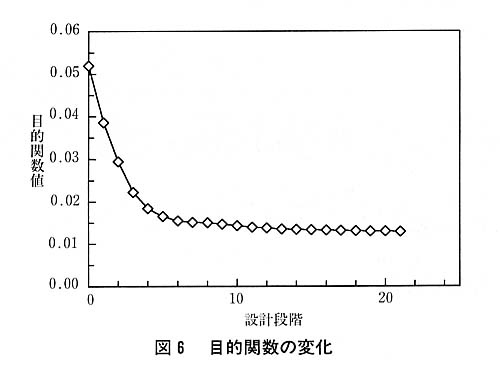
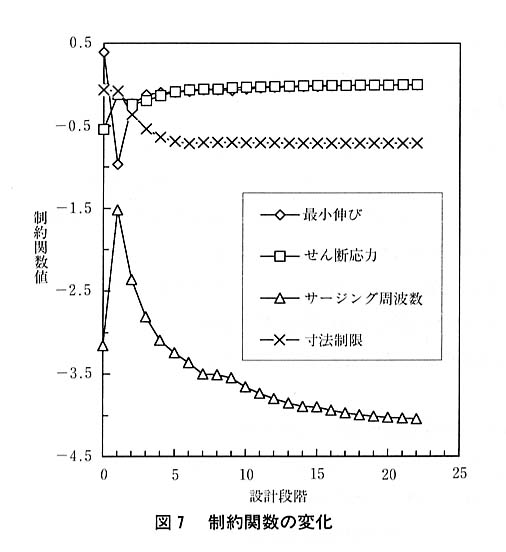
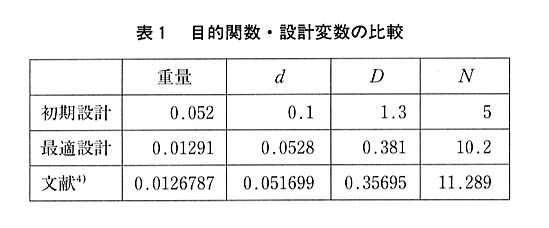
ε=3%とする。コイルばねの形状と各反復に対する設計変数の変化を図５に示す。図６にはこの例題における目的関数の変化を示す。目的関数は最初の数回の反復でほぼ一定の値まで減少することがわかる。図７には無次元化した4本の制約関数値の変化を示す。制約条件に違反しない設計はすべての制約値がゼロ以下でなければならない。図７から，例題ではすべての制約条件に違反しないで最適解が得られることがわかる。表１には最適解と目的関数値を文献4)の結果と併せて示す。この例題について両者はよい一致を示すことがわかる。

1. ①　設計最適化を目的とした汎用オプティマイザを開発した。このプログラムは機械設計に関する意思決定を解決する強力なツールとして活用することができる。
2. ②　機械要素設計への具体的な適用事例を通じてプログラムの有効性を検証し、良好な結果を得た。

最適設計は必然的に情報のやりとりをグラフィカルユーザインタフェースを使用して行うところに特徴がある。利用者と対話しながら最適化を行うプログラムが実用上望ましいと考えられる。

今後は各設計段階に利用者が介入することができるリスタート機能や感度係数の自動計算機能，さらに利用者がFortranで記述した感度係数を差分を用いて検証する機能などを追加する必要があると思われる。

〈参考文献〉

1)　寺島：最適設計のための非線形計画法プログラムの開発(その1)，職業能力開発報文誌第8巻1号, 1996

2)　Kelley, J.E.：The Cutting-Plane Method for Solving Convex Programs, J.SIAM8, p.703-712, 1960

3)　Baldur, J.E.：Structural Optimization by Inscribed Hyperspheres, J.Eng.Mech., ASCE, vol.98, No.EM3, p.503-508, 1972

4)　Arora, J.S.：Introduction to Optimum Design, McGraw-Hill, p.451-455, 1989